Cześć,
Deep Learning jest tym, co wszystkich fascynuje w sztucznej inteligencji. Sieci neuronowe. Skomplikowane połączenia ogromnej liczby “neuronów” które próbują odwzorować jak działa ludzki mózg. Poznajmy je trochę bliżej.
Znamy już trochę jeden z obszarów AI jakim jest Machine Learning (ML). Zrobiliśmy 2 proste projekty: kto przeżył katastrofę Titanica (problem klasyfikacji) oraz oszacowaliśmy ceny mieszkań w USA (problem regresji). Dziś przechodzimy dalej. Poznajemy kolejną z gałęzi ML jaką jest głębokie uczenie Deep Learning (DL). Również możemy ją zastosować do rozwiązania tych samych problemów: klasyfikacji i regresji.
Znowu przejdziemy sobie przez prosty kurs na Kaggle : https://www.kaggle.com/learn/intro-to-deep-learning
Zacznijmy od początku. Czym jest wspomniany “neuron”?
Neuron jest pojedynczą jednostką obliczeniową. Bardzo prostym elementem, który przeprowadza proste i szybkie obliczenie. Jedno. Najprostszy neuron ma jedno wejście, jedną “wagę” oraz jedno wyjście. Matematycznie możemy to zapisać jako funkcję liniową: y = wx + b.
Gdzie:
- x – wejście do neuronu (input) – tutaj mogą być podłączone wyjścia z poprzednich neuronów
- w – waga (weight) – parametr liczbowy który wzmacnia lub osłabia dane wejściowe (x) – taki mnożnik, zmieniając go możemy sterować pracą naszego modelu
- b – dodatek (bias) – drugi parametr neuronu niezależny od danych wejściowych (x)
To właśnie przez “dostrajanie” parametrów “w” oraz “b” dla poszczególnych neuronów, cała sieć “uczy się” aby rozwiązać dany problem.
Jeżeli dwa parametry zależą od siebie liniowo to taki prosty model wystarczy, aby obliczyć parametr wyjściowy.
Na przykład mając temperaturę w stopniach Celcjusza możemy wyliczyć odpowiednik w stopniach Fahrenheita za pomocą takiego neuronu: y = 9/5 * x + 32 (y – temperatura w stopniach Fahrenheita, x – temperatura w stopniach Celcjusza, waga “w” = 9/5 oraz bias “b” = 32).
Jeżeli parametr wyjściowy zależy od wielu parametrów wejściowych, wtedy je sumujemy: y = w0x0 + w1x1 + w2x2 + b. Możemy to zapisać jako y = suma(wagi * wejścia) + bias.
To jest właśnie pojedynczy neuron. Czyli taka prosta jednostka obliczeniowa (funkcja matematyczna: mnożenie i dodawanie). Mówiąc o sieci neuronowej mamy na myśli ich ogromną liczbę oraz połączenia pomiędzy nimi.
Dzielimy je dla czytelności na warstwy (layers). Możemy myśleć o warstwie jako o zbiorze neuronów o wspólnych wejściach (input) które przeprowadzają jakąś transformacje na danych. Są różne rodzaje takich warstw a różnią się one połączeniami i wagami które przydzielone są poszczególnym neuronom.
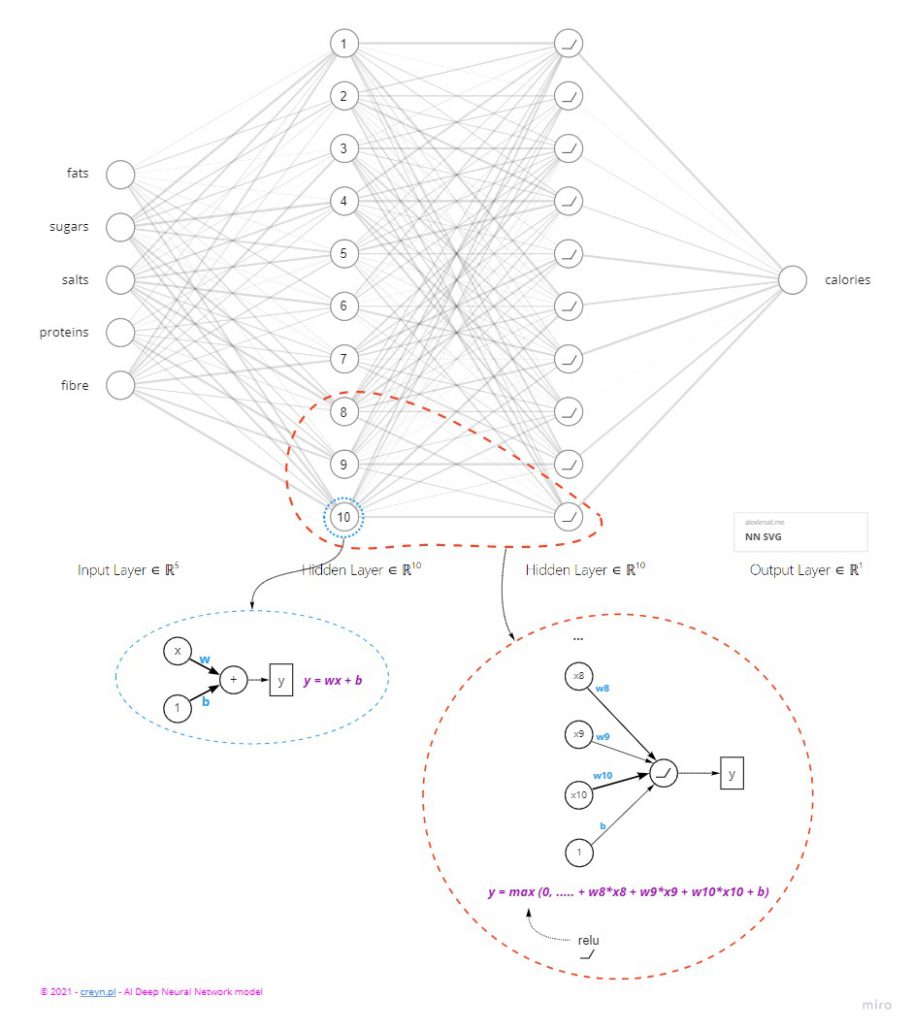
Liniowe neurony są najprostsze, ale nie będą wystarczające do rozwiązania bardzo skomplikowanych problemów. Potrzebujemy umieć przedstawić także inne zależności niż tylko liniowe. Pomagają w tym funkcje aktywacji (activation function). Najprostszą jest funkcja prostownikowa (rectifier function). Ma ona postać: max(0, x). Czyli zerujemy wszystkie wartości ujemne. Stosując ją do liniowego neurona mamy RELU – Rectifier Liner Unit. Czyli wyjściem z takiego neurona jest y = max(0, w*x + b).
Neurony i różne algorytmy pracują najlepiej w przedziale liczb <0, 1>. Czyli jeżeli mamy pewną wartość wejściową w przedziale 100 – 200 to należy wszystkie wartości przeskalować tak, aby najmniejsza wartość odpowiadała 0 a największa 1.
Uczenie sieci neuronowej
Ok, wiemy już z czego składa się sieć neuronowa. Wyobraźmy sobie, że tworzymy sieć z 5 wejściami, 2 warstw po 10 neuronów w każdej oraz 1 wyjściem (jak na diagramie powyżej). Jak wyglądają poszczególne wagi “w”? Otóż na początku są losowe. Nasza sieć jeszcze niczego się nie nauczyła. Musimy ją dopiero nauczyć (wytrenować). Sieć musi wiedzieć czy obliczona wartość jest poprawna. Do tego celu stosuje się funkcję strat (loss function). Chodzi o to, żeby stwierdzić czy wartość jest poprawna. Do dyspozycji mamy różne algorytmy, m.in. znany już nam MAE (mean average error).
Jeżeli obliczona wartość jest błędna, sieć “dostraja” wartości poszczególnych wag “w” aby zbliżyć się do poprawnego wyniku. Ten proces to optymalizowanie (optimizer). Mając zbiór danych wejściowych dzielimy je na mniejsze zestawy (batch) i wpuszczamy je do modelu naszej sieci. Po każdym takim batchu sieć się optymalizuje. Potem bierzemy kolejny batch i kolejny. Jeżeli przejdziemy przez wszystkie przypadki testowe to właśnie skończyła się epoka (epoch) a sieć nauczyła się już trochę rozwiązywać nasz problem. Cały proces zaczyna się od nowa. A kończy gdy poprawność naszej sieci przez kilka epok nie będzie się już zwiększać.
Czyli epoka zawiera wiele losowych zestawów z danych treningowych. Po każdym zestawie jest optymalizacja oparta na różnicy obliczonej wartości oraz tej prawdziwej. Fajnie jest to pokazane w tutorialu na Kaggle. Dlatego warto go chociażby przeklikać. Tym bardziej, że są poruszane też takie tematy jak: zbyt słabe wytrenowanie (underfitting) oraz “przetrenowanie” (overfitting). Opisane są też takie warstwy jak “dropout” (losowo wyrzucamy niektóre neurony, aby model nie utrwalał złych połączeń a tylko te dobre – pomaga na overfitting).
Sieć neuronowa nie jest bardzo skomplikowana. Składa się po prostu z ogromnej liczby neuronów. Każdy neuron jest bardzo prosty i szybko wykonuje operacje. Ucząc sieć dostrajamy poszczególne neurony i połączenia między nimi. Model trenuje się przez wiele epok, każda zawiera wykonanie operacji na danych podzielonych na zbiory batchy. Po każdym batchu na podstawie funkcji strat (loss) wracamy do modelu i dostrajamy wagi. Tak, aby błąd obliczeń modelu zbliżał się do zera.
Ciekawe linki
Na koniec kilka ciekawych linków z których skorzystałem
Omawiany tutorial: https://www.kaggle.com/learn/intro-to-deep-learning
Na tej stronie możesz sobie wygenerować przykładową sieć i zobaczyć jak dużo połączeń się w niej znajduje: http://alexlenail.me/NN-SVG/index.html. Skorzystałem z niej aby wygenerować swoją sieć na diagramie.
Tu z kolei możesz zobaczyć różne funkcje aktywacji dla neuronów: https://dashee87.github.io/deep%20learning/visualising-activation-functions-in-neural-networks/. Każda z tych funkcji lepiej pasuje do różnych rzeczy.
Bardzo fajnie przedstawione tworzenie i nauka sieci neuronowej. Do dyspozycji są różne problemy (klasyfikacja i regresja) oraz zbiory danych. Możemy dodawać parametry wejściowe, tworzyć dodatkowe warstwy a nawet modyfikować wagi i biasy neuronów. Widzimy jak sieć uczy się przez wiele epok i jak staje się coraz lepsza. https://playground.tensorflow.org/
Paweł
Wpis pochodzi z newslettera. Jeżeli chcesz dostawać podobne informacje na swojego mejla uzupełnij poniższy formularz. W każdej chwili możesz się wypisać.


